麦克斯韦方程组和麦克斯韦关系式有什么区别？

麦克斯韦方程组是电场和磁场的基本工具，而麦克斯韦方程组则侧重于温度、压力、体积和熵等热力学量。有关 Maxwell 方程组的更多信息，请参阅“Maxwell 方程组的基本原理是什么，它们与 TENG 有何关系？

Maxwell 的关系式为设计人员提供了一个强大的工具，用于分析内燃机或数据中心冷却等热力学系统。与 Maxwell 方程组一样，Maxwell 的关系式也基于偏导数。这些关系描述了热力学量的二阶偏导数的对称性。

麦克斯韦关系式直接或间接涵盖八个热力学量，包括压力 （P）、体积 （V）、温度 （T）、以焦耳/开尔文 （J/K） 为单位的熵 （S）、以焦耳/开尔文 （J/K） 为单位的内能 （U）、焓 （H）、亥姆霍兹自由能 （F） 和吉布斯自由能 （G）（图 1）。P、V 和 T 是简单量。其他热力学量更复杂，因此麦克斯韦关系很重要。

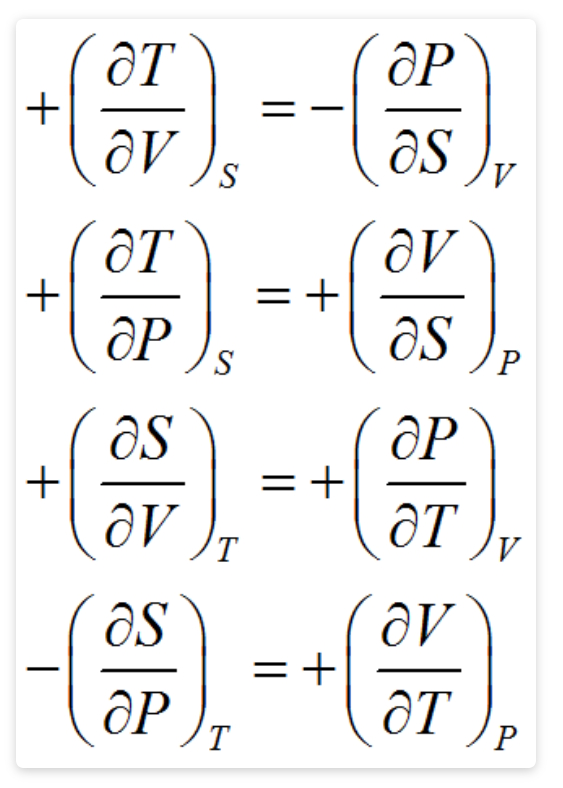
图 1.构成 Maxwell 关系的方程。图片来源：冶金与材料科学)

例如，焓 （H） 测量系统的总热含量，定义为其内能 （U） 与压力 （P） 和体积 （V） 的乘积之和：H = U + PV。亥姆霍兹自由能 （F） 测量在恒定温度和体积（定义为 F = U – TS）下从封闭系统获得的有用功。

吉布斯自由能 （G） 用于预测给定温度下过程的自发性;它被定义为 G = H – TS，或 ∂G = ∂H – T∂S：

• 当 ∂G < 0 时，该过程是自发的（首选）。

• 当 ∂G > 0 时，该过程是非自发的（不受欢迎）。

• 如果 ∂G = 0，则过程处于平衡状态。

麦克斯韦关系不仅仅是一个有趣的数学练习;它们很实用，使设计人员能够在设计热力学系统时用更容易测量的量代替难以测量的量。

热力学方

“热力学正方形”是一种助记符图，科学家和设计师可以使用它来绘制热力学电位（如 U、H、F 和 G）与相应的自然量（如 T、P、V 和 S）之间的关系。它最初是由德裔英国物理学家 Max Born 提出的。

在图 2（a） 中，自然变量 P、T、V 和 S 位于拐角处，U、F、G 和 H 位于其相应自然变量之间的边上，G 位于 P 和 T 之间，U 位于 V 和 S 之间，依此类推。此外，还有两个箭头，一个从 S 指向 T，另一个从 P 指向 V，用于识别每个电位的微分关系中的正负符号。

这个广场是为了建立麦克斯韦的关系而设计的。例如，图 2（b） 显示了如何推导 （∂T= ∂V）S和 （∂P= ∂S）V.在这种情况下，一个终端节点有一个指向它的箭头，而另一个终端节点没有。发生这种情况时，Maxwell 关系需要一个负号：（∂T= ∂V）S= -（∂P= ∂S）V.

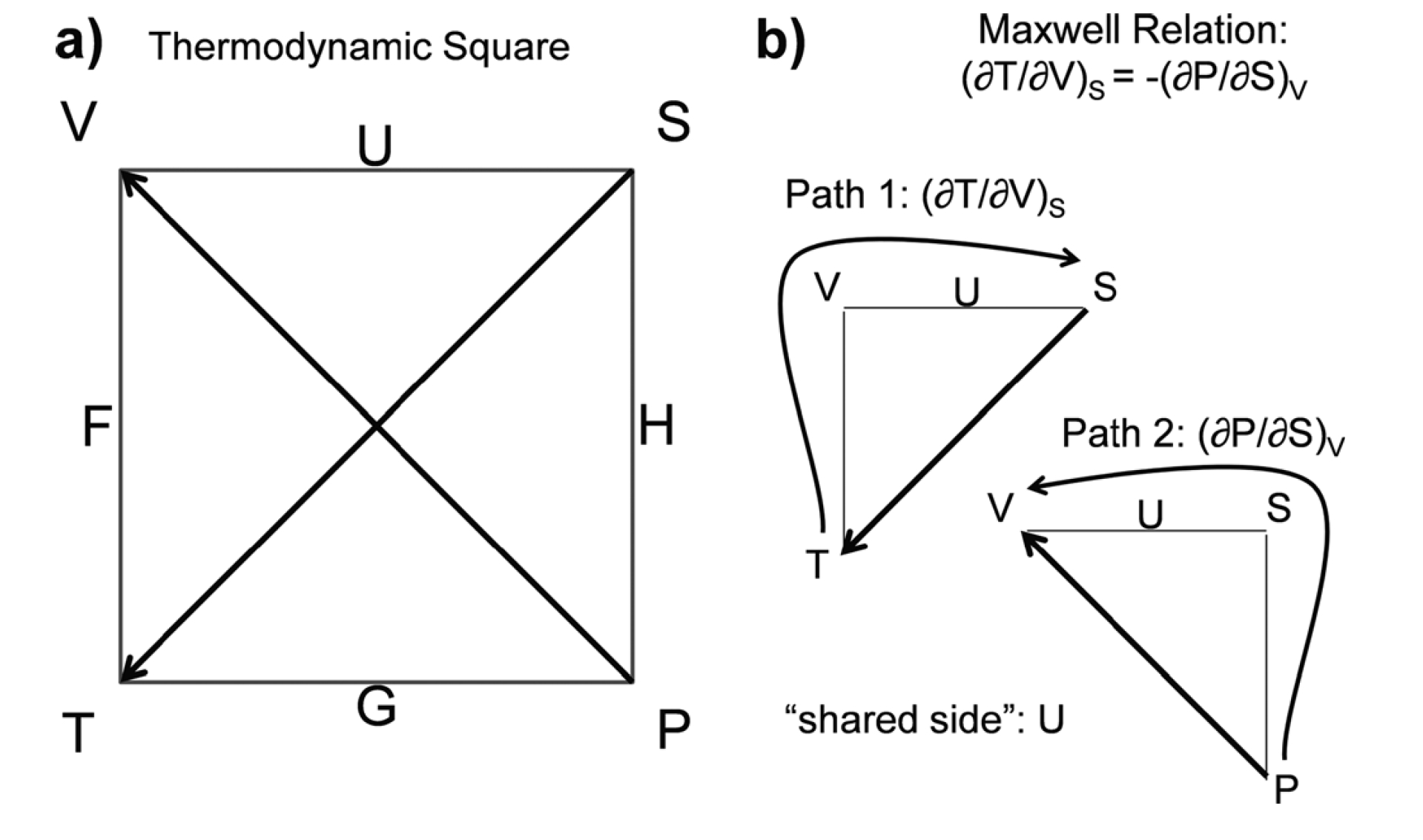图 2.热力学平方 （a） 以及它如何用于构建麦克斯韦关系 （b）。图片来源：维克森林大学)

冷却数据中心

Maxwell 的关系式可以描述用于数据中心冷却的 Carnot 循环。Carnot 模型代表了将热量转化为功或在两个温度之间进行冷却的最大可能效率。

麦克斯韦关系基于可逆性概念，而卡诺循环是一个可逆过程，因此非常适合使用麦克斯韦关系进行分析。卡诺循环由四个阶段组成（图 3）。

1. 等温（恒温）膨胀是指冷却气体在保持恒定温度并增加熵的同时吸收热量，导致气体膨胀并执行功。

2. 当气体继续膨胀而不与周围环境进行热交换时，就会发生绝热（无传热）膨胀，从而导致气体温度下降和熵恒定。

3. 等温压缩从气体中排出热量，同时降低熵并保持恒定温度。

4. 绝热压缩是最后阶段，气体被压缩而不传热。这提高了气体的温度，同时保持恒定的熵并使系统恢复到其起始状态。

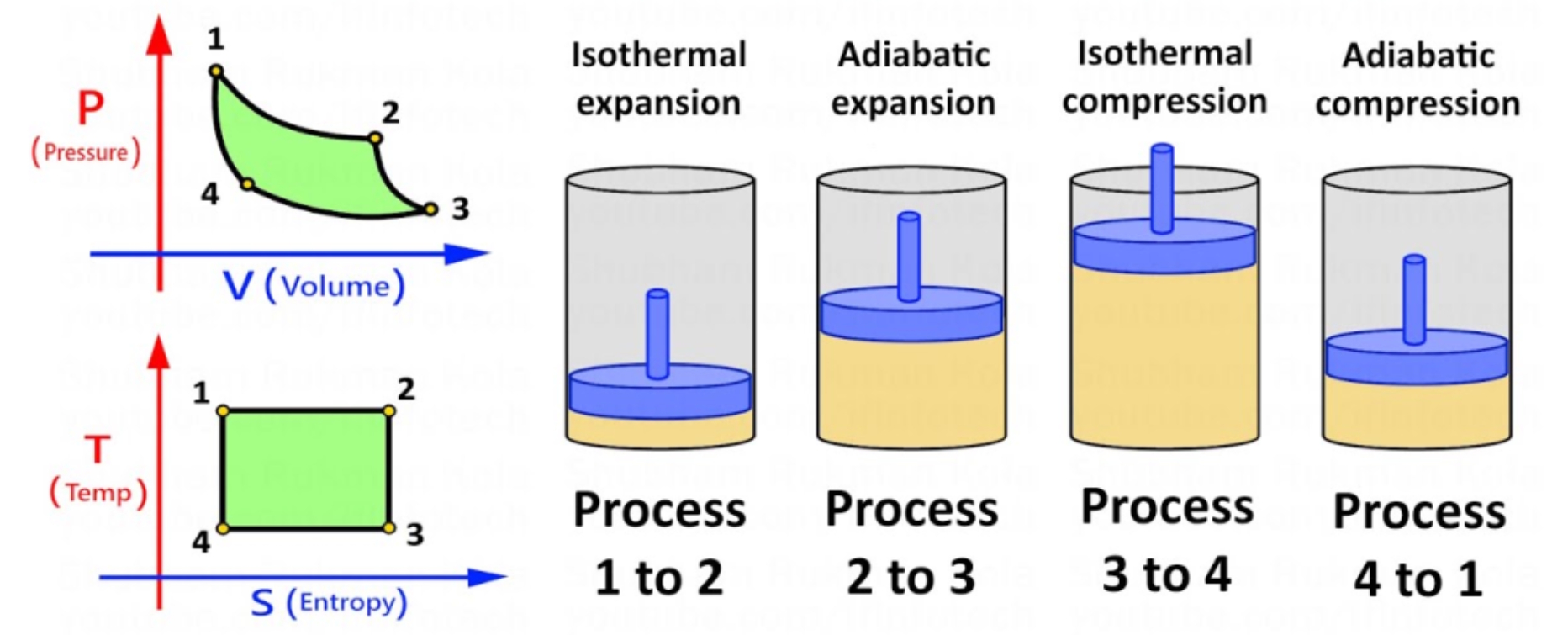图 3.在卡诺周期的四个阶段中，P & V之间以及T&S之间的关系。（图片：Paradigm Cooling)

总结

麦克斯韦关系使设计人员在设计热力学系统时，能够将焓、亥姆霍兹自由能和吉布斯自由能等难以测量的量替换为温度、体积和压力等易于测量的量。使用热力学正方形可以很容易地记住这些关系，它们是设计数据中心冷却器等系统的实用工具。